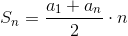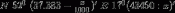 Zaloguj się, by zobaczyć współrzędne.
Zaloguj się, by zobaczyć współrzędne.
 5x znaleziona
5x znaleziona  0x nieznaleziona
0x nieznaleziona  0 komentarze
0 komentarze  2 obserwatorów
2 obserwatorów  Oceniona jako: znakomita
Oceniona jako: znakomita
aby zobaczyć współrzędne oraz
mapę lokalizacji skrzynki
 Atrybuty skrzynki
Atrybuty skrzynki




 Opis
PL
Opis
PL
Matematyczne Tropy - Trop nr 3
W każdym z trzech etapów znajdziesz kartkę z literą, która wraz z literami ze skrzynek Matematyczne Tropy nr 1 i 2 oraz skrzynki finałowej utworzą hasło. W pierwszych dwóch znajdziesz też informację jak dotrzeć do kolejnego etapu.
Etap I:
Anegdota o małym Gaussie: Gdy późniejszy "książę matematyków" Carl Friedrich Gauss był małym chłopcem i dopiero zaczynał naukę w szkole, wraz z innymi dziećmi otrzymał za zadanie policzenie sumy liczb od 1 do 100. Nauczyciel miał rzecz jasna nadzieję na dość długą chwilę spokoju, bo w końcu dodanie pod kreską tylu liczb, powinno było zająć dzieciom sporo czasu. Niestety, a może właśnie "stety", niezwykle biegły w rachunkach i nieprzeciętnie zdolny Gauss rozwiązał to zadanie niemal natychmiast. Nauczyciel długo wpatrywał się z niedowierzaniem na kartkę z takim oto rozwiązaniem:
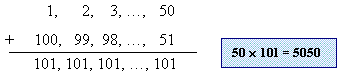
Żródło: https://edux.pjwstk.edu.pl/mat/224/lec/main34.html
Rozwiązanie to korzysta z wzoru na sumę 100 wyrazów ciągu arytmetycznego o a1 =1 i an = 100 oraz różnicy r=1.
Wzór ten przedstawia się następująco:
![]()
Wykorzystaj ten wzór do rozwiązania zadania:
Koszt robót przy drążeniu studni przedstawia się następująco: pierwszy metr kosztuje 100 złotych, a każdy następny o 10 złotych drożej niż poprzedni. Ile będzie kosztowało wywiercenie studni o głębokości 25 m.
Adres skrzynki otrzymasz podstawiając wynik zadania do wzoru:
![]()
English version:
In each of the three stages you will find a card with a letter, which along with the letters from the caches Mathematical Clues No. 1 and 3 and the final cache will create a password. In the first two you will also find information on how to reach the next stage.
First stage:
The Gaussian Mathematical Anecdote:
When Carl Friedrich Gauss (who was later called "The Prince of mathematicians") was a little boy and had just started school, he was given along with other children, the task of counting the numbers from 1 to 100. The teacher obviously hoped that it will take them a long time to complete it because there were so many numbers to add. Unfortunately unusually proficient in the calculus and unquestionably capable Gauss, solved this task almost immediately. The teacher stared incredulously at the paper with such a solution:
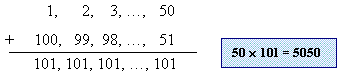
In this solution Gauss used the formula for a sum of n numbers of arithmetic sequence
as you can see below;
![]()
Use this pattern to solve the following task:
The cost of drilling wells is as follows: the first meter costs 100 zlotys, and the next one is 10 zloties more expensive than the previous one. How much will it cost to drill a well 25 m deep?
The address of the cache you can receive by substituting the result of the task x to the formula:
![]()
 Dodatkowe waypointy
Dodatkowe waypointy
| Etap | Symbol | Typ | Współrzędne | Opis |
|---|---|---|---|---|

|
Parking | --- | Skrzyżowanie dróg | |
| 1 |

|
Punkt fizyczny | --- |
Mała skrzynka zawierająca kartkę z literą oraz instrukcję dotyczącą sposobu dotarcia do następnego etapu. A small cache where you can find a card with a letter and information on how to reach the next stage. |
| 2 |

|
Punkt fizyczny | --- |
Mała skrzynka zawierająca kartkę z literą oraz instrukcję dotyczącą sposobu dotarcia do następnego etapu. A small cache where you can find a card with a letter and information on how to reach the next stage. |
| 3 |

|
Punkt fizyczny | --- |
Mała skrzynka zawierająca kartkę z literą oraz logbook A small cache where you can find a card with a letter and logbook. |
 Dodatkowe informacje
Dodatkowe informacje
 Obrazki/zdjęcia
Obrazki/zdjęcia
 Wpisy do logu:
Wpisy do logu:
 5x
5x
 0x
0x
 0x
0x